Definition of a logarithm

If

$x> 0$

and there is a constant

$b\ne 1$

, then

$y=lo{g}_{b}x$

, then  if and only if

$b^y=x$

In the equation

$lo{g}_{b}x$

, y is referred to as the logarithm, b is the base, and x is the argument.

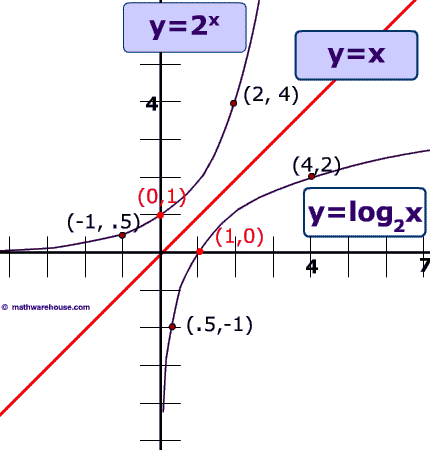
The notation  is read “the logarithm (or log) base b of x .” The definition of a logarithm indicates that a logarithm is an exponent

$y=lo{g}_{b}x$

is the logarithmic form of

$b^y=x$ $b^y=x$ $b^y=x$

is the exponential form of

$y=lo{g}_{b}x$

Example
1 Write each equation in its exponential form.

1. 1. 1.      a.
         $2=lo{g}_{7}x$      b.

         $3=lo{g}_{1}0〖(x+8)〗$c.

         $lo{g}_{5}125=x$

2 Write the following in its logarithmic form:

$x=〖25{〗}^{(}1/2)$

Solution:

Use the definition

$y=lo{g}_{b}x$

if and only if

$b^y=x$

(a)

$2=lo{g}_{7}x$

if and only if

$7^2=x$

(b).

$3=lo{g}_{1}0〖(x+8)〗$

if and only if

$〖10{〗}^3=x+8$

(c)

$lo{g}_{5}125=x$

if and only if

$5^x=125$

2. Use the definition
   $b^y=x$if and only if

   $y=lo{g}_{b}x$

$x=〖25{〗}^{(}1/2) if and only if$ $1/2=lo{g}_{2}5x$

EQUALITY OF EXPONENTS THEOREM

If b is a positive real number

$(b\ne 1)$

such that

$b^x=b^y, then x=y$

Example:

evaluate

$lo{g}_{2}32=x$

Solution: Use the definition

$y=lo{g}_{b}x$

if and only if

$b^y=x$ $x=lo{g}_{2}32$

if and only if

$2^x=32$

⇒

$2^x=2^5$

⇒     Thus, by Equality of Exponents,

$x=5$

PROPERTIES OF LOGARITHMS

$b\ne 1$

If b, a, and c are positive real numbers,

, and n is a real number, then:

1. Product:
   $lo{g}_b〖(a\times c)〗=lo{g}_{b}a+lo{g}_{b}c$
2. Quotient:
   $lo{g}_b〖a/c〗=lo{g}_{b}a–lo{g}_{b}c$
3. Power:
   $lo{g}_b〖a^n〗=n.lo{g}_{b}a$
4. $lo{g}_{a}1=0$
5. $lo{g}_{b}b=1$
6. Inverse 1:
   $lo{g}_b〖b^n〗=n$
7. Inverse 2:
   $b^{l}o{g}_{b}n=n,n>0$
8. One-to-one:
   $lo{g}_{b}a=lo{g}_{b}c$ $if and only if a=c$
9. Change of base:
   $lo{g}_{b}a=lo{g}_{c}a/lo{g}_{c}b=loga/logb=lna/lnb$

 Examples

1. Use the properties of logarithms to rewrite each expression as a single logarithm:

(a)

$2lo{g}_{b}x+1/2lo{g}_b〖(x+4)〗$

(b)

$4lo{g}_b〖(x+2)〗–3lo{g}_b〖(x–5)〗$

2. Use the properties of logarithms to express the following logarithms in terms of logarithms of x, y and z

(a)

$lo{g}_b〖\left(x{y}^2\right)〗$

(b)

$lo{g}_b〖(x^2\surd y)/Z^5〗$

Solutions: 1. Use the properties of logarithms to rewrite each expression as a single logarithm:

(a)

$2lo{g}_{b}x+1/2lo{g}_b〖(x+4)〗=lo{g}_b〖x^2〗+lo{g}_b〖〖(x+4){〗}^{(}1/2)〗$

power property

$=lo{g}_b〖[x^2〖(x+4){〗}^{(}1/2)〗]$

product property

(b)

$4lo{g}_b〖(x+2)〗–lo{g}_b(x–5)=lo{g}_b〖(x+2{)}^4〗–〖3log{〗}_b〖〖(x+4){〗}^3〗$

power property

$=lo{g}_b〖〖(x+2){〗}^4/〖(x–5){〗}^3〗$

quotient property

2. Use the properties of logarithms to express the following logarithms in terms of logarithms of x, y and z

(a)

$lo{g}_b〖x{y}^2〗=lo{g}_{b}x+lo{g}_b〖y^2〗$

product property                       ⇒

$lo{g}_b〖x{y}^2〗=lo{g}_{b}x+lo{g}_b〖y^2〗$

(b)

$lo{g}_b〖(x^2\surd y)/Z^5〗$ $=lo{g}_b〖(x^2\surd y)〗–lo{g}_b〖Z^5〗$

quotient property

$=lo{g}_b〖x^2+〗lo{g}_b\surd y–lo{g}_b〖Z^5〗$

product property

$=〖2lo{g}_b〗〖x+〗lo{g}_b\surd y–5lo{g}_{b}Z$

power property

COMMON LOGS

A common logarithm has a base of 10. If there is no base given explicitly, it is common. You can easily find common logs of powers often. You can use your calculator to evaluate common logs.

NATURAL LOGS

A natural logarithm has a base of e. We write natural logarithms as ln. In other words,

$lo{g}_{e}x=lnx$

.